Parallelizzazione dell'apprendimento di una rete neurale su Cpu-OpenMP e Gpu-NvidiaCUDA

06/08/2017 2287 parole 11 minuti

/it/neural-network-cuda/memoria_nvidia.png

Contenuti

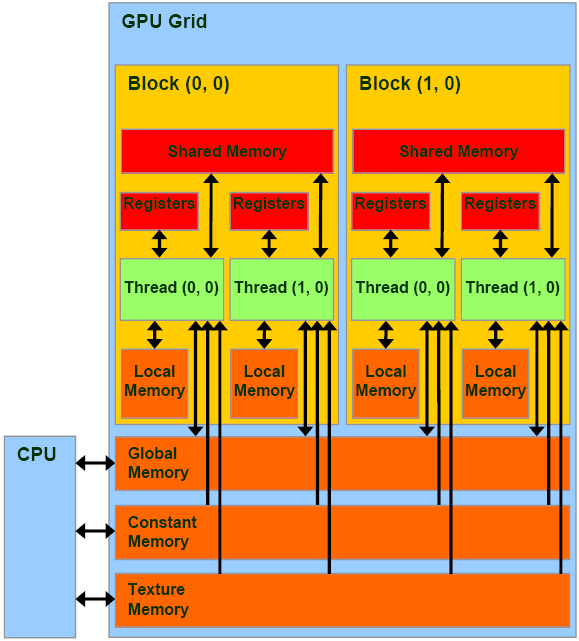
Obiettivo

L’obiettivo è ottimizzare e parallelizzare un programma fornito in C per il riconoscimento della scrittura a mano libera per mezzo di una rete neurale a retropropagazione. E’ richiesto che venga prodotta una versione parallelizzata su processore che sfrutti al meglio la libreria per compilatore OpenMP ed una che sfrutti la tecnologia Nvidia Cuda. E’ inoltre richiesto che venga posta particolare attenzione all’accesso alla memoria nella versione Cuda.

Ambiente di sviluppo

La versione del programma OpenMP parallelo è stata ottenuta sviluppando e eseguendo test su un computer dotato di Intel i7700k Kaby Lake ed una scheda video ATI R9 290 (causa per la quale la versione CUDA è stata sviluppata su un altro sistema).

La versione CUDA è stata sviluppata e testata su una Nvidia Quadro FX3800 1GB con Compute Capability di 1.3 abbinata ad un Intel I3 di terza generazione Ivy Bridge. L’IDE utilizzato è Atom, il makefile utilizzato è disponibile insieme al codice sorgente consegnato. L’analisi dei risultati è stata eseguita tramite lo strumento “perf”.

Versione ottimizzata monothread

Prima di parallelizzare il programma è stato utile avere un primo approccio improntato sull’ottimizzazione del codice già esistente, rimanendo con un unico flusso di esecuzione. Per prima cosa sono stati posti dei timer fra i vari macroblocchi di codice del programma per andare a misurare il peso computazionale di ognuno (dati disponibili in “nnml_analyzed-input.ml.log”).

E’ stato subito evidente come la penultima parte, riportata di seguito, fosse la porzione di programma che richiedeva più tempo per essere eseguita (circa 220 secondi).

Esempio di ottimizzazione sul penultimo macro blocco di codice

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


// prima dell'ottimizzazione
for(h=NumHL; h>0; h--) { // ciclo a
    for( j = 1 ; j <= nupl[h] ; j++ ) {  // ciclo b
      DeltaWeightH2H[h-1][0][j] = alpha * DeltaWeightH2H[h-1][0][j];
      for( np = 0 ; np < NumPattern ; np++ ) { // ciclo c
        p = ranpat[np];
        DeltaWeightH2H[h-1][0][j] += eta * DeltaH2H[h-1][p][j];
      }
    }
    for( j = 1 ; j <= nupl[h] ; j++ ) { // ciclo d
      for( i = 1 ; i <= nupl[h-1] ; i++ ) {  // ciclo e
        DeltaWeightH2H[h-1][i][j] = alpha * DeltaWeightH2H[h-1][i][j];
        for( np = 0 ; np < NumPattern ; np++ ) { // ciclo f
          p = ranpat[np];
          DeltaWeightH2H[h-1][i][j] += eta * ((h>1)?H2H[h-2][p][i]:Input[p][i-1]) * DeltaH2H[h-1][p][j];
       }
      }
    }
  }
// dopo l'ottimizzazione
for(h=1; h<=NumHL; h++) { // ciclo a
    i_max = nupl[h-1];
    j_max = nupl[h];
    for( i = 0 ; i <= i_max ; i++ ) { // ciclo b
      pointer32 = DeltaWeightH2H[h-1][i];
      for( j = 1 ; j <= j_max ; j++ )  //
        pointer32[j] *=alpha;
    }
    for( np = 0 ; np < NumPattern ; np++ ) { // ciclo f
      p = ranpat[np];
      DeltaH2H_h1_p = DeltaH2H[h-1][p];
      factor_x = ((h>1)?H2H[h-2][p]:Input[p]);
      pointer32 = DeltaWeightH2H[h-1][0];
      for( j = 1 ; j <= j_max ; j++ ) 
        pointer32[j] += eta * DeltaH2H_h1_p[j];
      for( i = 1 ; i <= i_max ; i++ ) { // ciclo e
        pointer32 = DeltaWeightH2H[h-1][i];
        factor_x_indexed = factor_x[((h>1)?i:i-1)] * eta;
        for( j = 1 ; j <= j_max ; j++ )  // ciclo d
          pointer32[j] += factor_x_indexed * DeltaH2H_h1_p[j]; 
      }
    }
  }

La prima ottimizzazione è stata quella di spostare il ciclo for “f” prima di “d”, in modo da permettere al processore di sfruttare la cache evitandogli di saltare da un punto all’altro di un array vasto (si noti che DeltaH2H e H2H hanno “p” come seconda dimensione, non ultima; a causa di questo quindi ponendo il ciclo più interno sulle “p”, ad ogni iterazione il processore lavora su porzioni di memoria spazialmente distanti).

Questa modifica da sola ha permesso di ridurre il tempo di esecuzione di quasi 150 secondi ed è solo un esempio di come si è operato su tutte le sezioni del codice, divise da timer numerati per individuare eventuali miglioramenti settoriali in seguito a modifiche.

Gran parte dell’ottimizzazione del codice infatti si è basata sull’ottimizzazione dell’accesso alla cache o sulla riduzione del numero di operazioni necessarie nei seguenti modi:

Andando a cambiare l’ordine di inclusione di cicli for in base alle variabili da aggiornare o leggere (versioni 2, 7, 17, 22).
Utilizzando ove necessario variabili di appoggio temporanee da aggiornare all’interno di cicli e poi salvare in memoria, evitando ad ogni iterazione di aggiornare inutilmente tale valore di memoria (3, 5, 10, 11, 13, 23, 31, 32, 33, 34).
Fondendo o dividendo in due cicli for per ottimizzare l’accesso alla memoria: cycle fusion o splitting (13, 14, 15).
Diminuendo le istruzioni da eseguire ripetutamente dentro i for, ad esempio sfruttando l’associatività delle operazioni +,* (26,27,28,29).
Abilitando i flag di ottimizzazione Ofast (include O3), -funroll-loops, -fbounds-check, -funswitch-loops nel makefile (30).

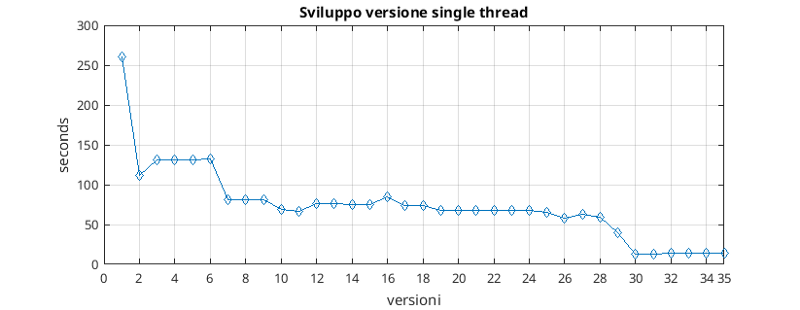
Come si può vedere dal grafico delle versioni, lo sviluppo di questa versione ottimizzata ha permesso sul nostro sistema di abbattere i tempi di esecuzione da più di 250 secondi a poco più di 10.

Versione OpenMP

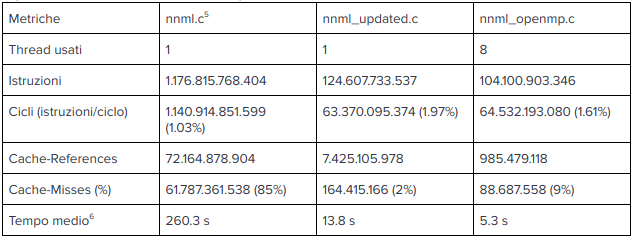
La versione OpenMP parallela è stata sviluppata a partire dalla versione ottimizzata, in quanto costituiva una buona base da parallelizzare dato il numero di miglioramenti già apportati.

Le versioni 10, 11 costituiscono la parallelizzazione del blocco centrale del programma. In questa fase è stato reso necessario l’utilizzo della primitiva “omp atomic” per preservare l’integrità del valore globale dell’errore. Il ritardo provocato dalla serializzazione dell’operazione di aggiornamento dell’errore viene bilanciato da un vantaggio considerevole nei tempi di esecuzioni dovuto alla parallelizzazione dei cicli for. Inoltre è ove necessario si è fatto largo uso di funzionalità come la “omp simd” (che permette la vettorializzazione dei cicli single thread) e la “omp reduction” (ad esempio per ottimizzare cicli di somma di una variabile).

E’ stata posta molta attenzione inoltre alla “visibilità” delle variabili nei blocchi di codice parallelo di OpenMP. L’obiettivo era di minimizzare l’interazione fra thread tramite variabili (dichiarando le variabili come private o firstprivate), in modo da massimizzare conseguentemente il parallelismo.

La parte di inizializzazione del programma, durante il quale vengono letti dei file, è stata parallelizzata utilizzando la funzione “omp task”, permettendo un piccolo guadagno sul tempo di esecuzione (5, 12, 13, 14).

Il penultimo ciclo ottimizzato, preso in esame nel capitolo precedente, è stato modificato per evitare l’uso di operazioni atomiche che avrebbero annullato il beneficio dell’esecuzione parallela. Grazie al lavoro svolto si è ottenuto comunque un miglioramento delle performance anche in quella porzione di codice (20, 21, 22, 23).

Infine sono stati testati diversi tipi di scheduler per i blocchi “omp parallel for” ed è stato scelto quello che ha restituito i miglior risultati sul sistema di test (24).

Versione Cuda

La versione CUDA è stata sviluppata a partire da “nnml_openmp.c” e “nnml_updated.c”. Utilizzando la suddivisione in porzioni di codice già utilizzata per lo sviluppo, si è proceduto andando ad affiancare ad ogni blocco un kernel CUDA con funzionalità equivalenti e con invocazioni di funzioni di copia verso il device e dal device prima e dopo l’esecuzione gpu, in modo da poter verificare la corretta implementazione su scheda video della porzione analizzata.

A causa di questo metodo di lavoro che ha visto affiancare codice CPU a codice GPU, ed al fatto che il sistema su cui è stato sviluppato è molto meno performante di quello utilizzato per le altre parti (la funzione che verifica la correttezza dell’output del programma impiega molto più tempo, avrebbe rallentato lo sviluppo), non è stato possibile tenere un log dello sviluppo dell’applicazione.

La scelta architetturale di suddividere il programma in numerosi kernel è stata dettata sia dalla maggiori performance possibili andando a scegliere il numero di thread ottimale per ogni porzione di codice, sia dal tempo massimo di esecuzione di un kernel fornito dal driver della scheda video prima di sollevare una eccezione di timeout.

Gestione di Array

Come da “Best Practice” Cuda, gli array multidimensionali utilizzati sono stati implementati come array ad una dimensioni, andandoli ad “appiattire”. Questa scelta ha condotto alla necessità di calcolare il corretto posizionamento di celle multidimensionali proiettate su un unico grande array 1d. Inoltre alcuni vettori a 3 dimensioni utilizzati dall’algoritmo fornito non sono costituiti da liste di matrici omodimensionali, ma con matrici di diverse lunghezze, andando a complicare l’eventuale calcolo dell’indice sulla struttura appiattita (le celle sono state scritte in un unico grande vettore, ponendo le righe una dopo l’altra formando matrici, anch’esse una dopo l’altra formando il vettore 3d).

Il problema è stato risolto con l’introduzione di strutture dati che potessero inglobare questa complessità:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


struct Vector_3D {
    VECTOR_TYPE * vector;
    int x_dim;
    int y_dim[MAX_SIZE_VECTOR];
    int z_dim[MAX_SIZE_VECTOR];
  };
struct Vector_2D {
    VECTOR_TYPE * vector;
    int rows;
    int cols;
  };

Con il puntatore vector si ha il puntamento all’array monodimensionale (su gpu o cpu) dell’array multidimensionale appiattito.

Nel caso due dimensioni sono stati indicati il numero di linee e di colonne, mentre nel caso 3D si è definito “x_dim” come il numero di matrici 2D e due vettori “y_dim” e “z_dim” rispettivamente array di numero di linee e di colonne delle matrici contenute nell’array 3D.

Il vantaggio di aver inglobato tutte le informazioni riguardo un vettore all’interno della struct risiede nella possibilità di costruire metodi che possano restituire l’indice richiesto passando come parametro solamente la struct in questione e le coordinate richieste, non preoccupandosi di richiamare ad ogni invocazione della funzione le reali dimensioni del vettore. Allo stesso modo sono state implementate funzioni per la copia in entrambe le direzioni fra device e host che necessitano come parametro solo delle struct degli array.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


__device__ static inline int index_3D_gpu
         (struct Vector_3D v, int x, int y, int z){
    int x_t = x;
    int index = y * v.z_dim[x] + z;
    for (;x_t>0;x_t--){
      index += v.z_dim[x_t-1] * v.y_dim[x_t-1];
    }
    return index;
  }
  __device__ static inline int index_2D_gpu
                       (struct Vector_2D matrix, int x, int y){
    return x*(matrix.cols)+y;
  }

Memorie GPU Utilizzate

[http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#device-memory-accesses](http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#device-memory-accesses)

Utilizzo della Shared Memory

Per garantire ottime performance in kernel che richiedono operazioni come la moltiplicazione fra matrici, con un gran numero di accessi alla memoria globale, è stato fatto largo uso di “Shared Memory”. Seguendo quanto spiegato in aula e disponibile nella documentazione Cuda sulla Shared Memory si è implementato l’algoritmo “Tiled” nel kernel 0, 1, 7, 8. L’idea è quella di precaricare porzioni di matrici in Shared Memory, in modo parallelo fra thread dello stesso blocco, per poi andare ad eseguire l’operazione richiesta sfruttando la velocità della Shared Memory (e l’accesso parallelo che tale memoria garantisce se senza conflitti).

Nel Kernel 2, 3 data la grandezza limitata di alcuni vettori in input è stato possibile caricare l’intera matrice direttamente in Shared Memory.

Utilizzo della Constant Memory

La “Constant Memory” si è rivelata utile in caso di variabili in sola lettura, come interi passati in input, accedute contemporaneamente da diversi thread, anche di diversi blocchi. Per un “half warp” leggere una variabile in Constant Memory è un’operazione parallela veloce quanto la lettura da un registro, con il vantaggio di non dover richiedere un registro per ogni thread.

E’ stata utilizzata in quasi tutti gli 11 kernel per costanti come “NumPattern”, “NumHL”, ”NumOutput”.

Utilizzo della Texture Memory

La Constant Memory è una memoria che permette operazioni di lettura molto veloci, ma è caratterizzata da una esigua capacità (attualmente 64KB). Alcuni vettori passati in input al programma come “ranpat” e “nupl” vengono acceduti dal programma in modo massivo dai thread e sempre in modalità lettura.

Purtroppo l’eccessiva grandezza del primo e la loro lunghezza non nota a tempo di compilazione hanno reso impossibile la loro allocazione in Constant Memory.

Per fortuna l’architettura CUDA mette a disposizione la “Texture Memory” che permette allocazione dinamica, è comune per tutti i blocchi (a differenza della Shared Memory, quindi non c’è replicazione di dati), sfrutta una cache nel chip (permettendo letture molto veloci) e offrendo prestazioni ottime in caso di accesso a dati spazialmente vicini (questi vettori vengono acceduti da molti thread contemporaneamente che ciclano su essi).

Operazioni Atomiche

Come per la versione OpenMP, è stato reso necessario l’uso dell’operazione di addizione atomica per il calcolo dell’errore globale. Data la volontà di mantenere il programma compatibile con versioni deprecate di Compute Capability come la 1.3, è stata utilizzata un’implementazione suggerita dalla documentazione Cuda della “atomicAdd” che sfrutta funzioni atomiche disponibili su tale versione di CC.

Per diminuire l’impatto negativo che un’operazione atomica non supportata dall’hardware nativamente poteva apportare al tempo di esecuzione, la somma atomica è stata inserita in un kernel che effettua la somma per riduzione prima all’interno dei vari blocchi di thread, e solo come riduzione finale utilizza la primitiva atomica.

Verifica della correttezza del programma

Al fine di verificare l’integrità dei moduli di calcolo del programma originario durante tutta la fase di sviluppo i kernel sono stati affiancati dal codice originario cpu, in modo da confrontare input e output. Come ulteriore prova di correttezza è stato utilizzato lo script fornito insieme alla traccia per la verifica dei file di output generati.

Un altro utile strumento per la verifica del programma Cuda è stato “cuda-memcheck”, disponibile nel toolkit Cuda, in grado di segnalare eventuali accessi in memoria non consentiti, sintomo di un malfunzionamento o implementazione errata.

Repository

https://gitlab.com/Ablablab/multi-many-core-1617

Riferimenti

[1] http://www.openmp.org/
[2] http://www.nvidia.it/object/cuda-parallel-computing-it.html
[3] Compilato senza ottimizzazioni del compilatore.
[4] Misurati tramite la funzione time di linux (bassa precisione), media di 10 run.
[5] Lo standard c99 risolve il problema permettendo di dichiarare struct con array di dimensione variabile int vec . Per compatibilità è stato scelto di dichiarare una grandezza massima in modo statico.
[6] http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#shared-memory
[7] http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#device-memory-accesses
[8] http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#atomic-functions