Implementation of the PREFIX SUM algorithm in Nvidia Cuda C environment

Implementation of the operation of PREFIX SUM inclusive in NvidiaCuda environment.

Objective

A C-Cuda program is supplied in which to insert the kernel to process the vector PREFIX SUM inclusive of a vector supplied in input. The developed kernel will have to use Shuffle operations. The program will therefore be compatible with Cuda devices with Compute Capabilities not lower than 3.0.

The PREFIX SUM problem has long been considered as an example of how an apparently serial problem can be parallelized. The two most famous algorithms that solve this problem allow to solve it with a complexity of O(n*logn) and O(n).

The developed algorithm is the one with greater complexity O(logn * n).

Development environment

The application was developed and tested on a Nvidia Quadro P6000 24GB with Compute Capability of 6.1. The IDE used is Atom, the makefile used is available together with the source code delivered.

Kernel Cuda

The kernel is currently invoked with a number of threads per block equal to 1024, this, in addition to constituting a technological limit of the CUDA architecture, allows for a maximum of 32 warps for each block and therefore being able to efficiently calculate the value with just one block returned as a result by the other warps in the block.

The algorithm is composed of 3 parts, based on the hierarchical organization of the Threads within the CUDA architecture.

1. WARP-level resolution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// sum in warp, <<= is a shift, it doubles the number 
   for (d=1; d<WARPSIZE; d<<=1) {
      others_int = __shfl_up(personal_int,d); // no need for syncthread,
      // shuffle instructions are executed at the same time for all warp
      if (threadId_warp >= d)
      personal_int += others_int;
    }
if (threadId_warp == 31) //last thread of warp store its value for other warps
    vector_block[warpId_block] = personal_int;
__syncthreads(); //data for single warp is updated

The problem of the Fixed Prefix Sum within each warp is fixed using shuffle statements. In this way the threads communicate with each other by “exchanging” the value contained by the registers, using a logarithmic number of steps according to the naive algorithm illustrated in the Cuda documentation.

2. Block level resolution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

if (warpId_block == 0){
      int other_warp, sum_warp = vector_block[threadId_warp];
for (d=1; d<WARPSIZE; d<<=1) {
        other_warp = __shfl_up(sum_warp,d);
        if (threadId_warp >= d) //maybe not needed
        sum_warp += other_warp;
      }
vector_block[threadId_warp] = sum_warp;
    }
__syncthreads();
    if(warpId_block>0)
      personal_int += vector_block[warpId_block-1];
    data[threadId_absolute] = personal_int;
__syncthreads();

The problem of the Prefix Sum within each block is solved, starting from the solutions of each warp. At the beginning of this phase, the first warp (all 32 threads that are part of it) collects the last value of each warp of the block and generates a Prefix Sum vector (a vector of 32 elements, built starting from the values of the last thread of each warp, following the algorithm illustrated in point 1). In this way each thread can add to its calculated value that of the previous warp, in order to solve the prefix sum within each block. The prefix sum performed by the first warp at the beginning of this phase was performed using the shuffle operations, exactly as for point 1. However, unlike point 1, the values were exchanged by the warps using a vector in Shared Memory.

3. Global resolution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

if(blockId == 0){ // first block is ready
      if(threadId_block == 0)
      atomicAdd(ready_counter, 1);
      return;
    }
if(blockId != 0 && threadId_block==0){
      int now = atomicAdd(ready_counter, 0);
      while(now < blockId){now = atomicAdd(ready_counter, 0);} // waiting for prev block
    }
    __syncthreads();
personal_int += data[(blockId)*blockDim.x - 1];
    data[threadId_absolute] = personal_int;
__syncthreads();
    if(threadId_block == 0){
      atomicAdd(ready_counter, 1); // this block is ready, next one can start
    }

All that is left is to merge the results for each block. In fact, each thread only has to add the sum of all the last elements of the previous blocks to the value calculated before to obtain the final result. The problem is that communication between blocks is not possible via the fast Shared Memory, furthermore it is not possible to use synchronization primitives like “__syncthreads()”. The main problem is that the Cuda architecture does not specify the order of execution of the various blocks, therefore it may happen that a block i has reached this stage before block i-1, in this way the value sought by the threads of block i is not it’s still available.

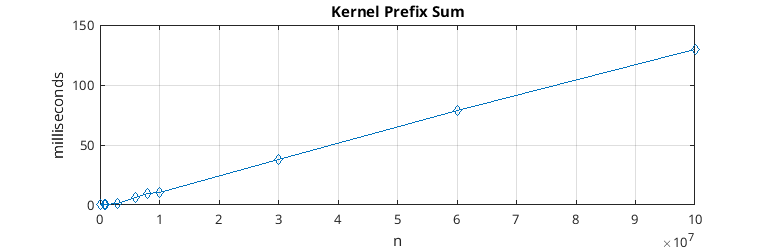
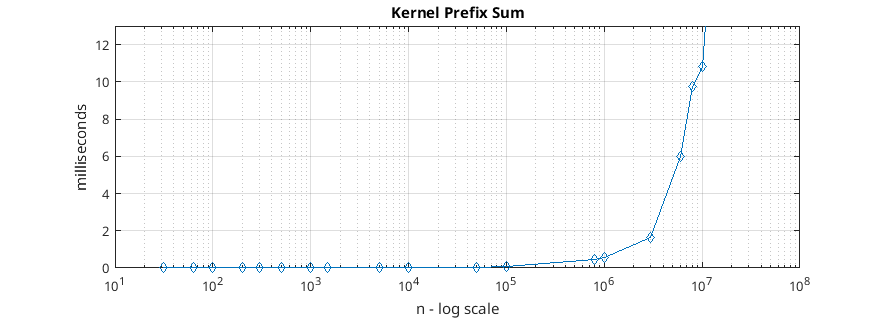
To synchronize the blocks, the primitive “atomicAdd” was used on a global memory value. As soon as phase 2 concludes, the first block increments by one unit a global counter initially set to 0 by means of the aforesaid primitive. The second block starts phase 3 by waiting (the first thread calls atomicAdd on the global counter, increasing it by 0, the other threads of the block wait for the first with the “__syncthreads()") for the counter to become equal to 1. Once the first block increments the counter, the threads in the second block are “unblocked” and update their value by retrieving it from the last item the first block is responsible for. Once all the elements of the block have been updated, it increments the counter by unlocking the third thread block. The mechanism repeats itself until all the blocks have been awakened and have done their sum for each thread, thus returning a correct vector that solves the Prefix Sum problem.

Repository

The repository with all the source code is available at: https://gitlab.com/Ablablab/multi-many-core-1617